| java.lang.Object | |
| ↳ | android.hardware.SensorEvent |
This class represents a Sensor event and
holds informations such as the sensor's type, the time-stamp, accuracy and of
course the sensor's data.
Definition of the coordinate system used by the SensorEvent API.
The coordinate-system is defined relative to the screen of the phone in its default orientation. The axes are not swapped when the device's screen orientation changes.
The X axis is horizontal and points to the right, the Y axis is vertical and points up and the Z axis points towards the outside of the front face of the screen. In this system, coordinates behind the screen have negative Z values.
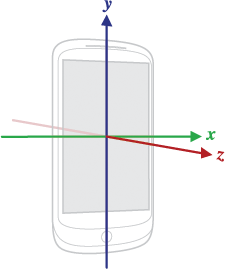
Note: This coordinate system is different from the one used in the Android 2D APIs where the origin is in the top-left corner.
| Fields | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| accuracy | The accuracy of this event. | ||||||||||
| sensor | The sensor that generated this event. | ||||||||||
| timestamp | The time in nanosecond at which the event happened | ||||||||||
| values |
The length and contents of the |
||||||||||
|
[Expand]
Inherited Methods | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 From class
java.lang.Object
From class
java.lang.Object
| |||||||||||
The sensor that generated this event. See
SensorManager for details.
The length and contents of the values array depends on
which sensor type is being monitored (see
also SensorEvent for a definition of the coordinate system used).
Sensor.TYPE_ACCELEROMETER:values[0]: Acceleration minus Gx on the x-axis
values[1]: Acceleration minus Gy on the y-axis
values[2]: Acceleration minus Gz on the z-axis
A sensor of this type measures the acceleration applied to the device (Ad). Conceptually, it does so by measuring forces applied to the sensor itself (Fs) using the relation:
In particular, the force of gravity is always influencing the measured acceleration:
For this reason, when the device is sitting on a table (and obviously not accelerating), the accelerometer reads a magnitude of g = 9.81 m/s^2
Similarly, when the device is in free-fall and therefore dangerously accelerating towards to ground at 9.81 m/s^2, its accelerometer reads a magnitude of 0 m/s^2.
It should be apparent that in order to measure the real acceleration of the device, the contribution of the force of gravity must be eliminated. This can be achieved by applying a high-pass filter. Conversely, a low-pass filter can be used to isolate the force of gravity.
public void onSensorChanged(SensorEvent event)
{
// alpha is calculated as t / (t + dT)
// with t, the low-pass filter's time-constant
// and dT, the event delivery rate
final float alpha = 0.8;
gravity[0] = alpha * gravity[0] + (1 - alpha) * event.values[0];
gravity[1] = alpha * gravity[1] + (1 - alpha) * event.values[1];
gravity[2] = alpha * gravity[2] + (1 - alpha) * event.values[2];
linear_acceleration[0] = event.values[0] - gravity[0];
linear_acceleration[1] = event.values[1] - gravity[1];
linear_acceleration[2] = event.values[2] - gravity[2];
}
Examples:
Sensor.TYPE_MAGNETIC_FIELD:Sensor.TYPE_GYROSCOPE:
values[0]: Angular speed around the x-axis
values[1]: Angular speed around the y-axis
values[2]: Angular speed around the z-axis
Typically the output of the gyroscope is integrated over time to calculate a rotation describing the change of angles over the timestep, for example:
private static final float NS2S = 1.0f / 1000000000.0f;
private final float[] deltaRotationVector = new float[4]();
private float timestamp;
public void onSensorChanged(SensorEvent event) {
// This timestep's delta rotation to be multiplied by the current rotation
// after computing it from the gyro sample data.
if (timestamp != 0) {
final float dT = (event.timestamp - timestamp) * NS2S;
// Axis of the rotation sample, not normalized yet.
float axisX = event.values[0];
float axisY = event.values[1];
float axisZ = event.values[2];
// Calculate the angular speed of the sample
float omegaMagnitude = sqrt(axisX*axisX + axisY*axisY + axisZ*axisZ);
// Normalize the rotation vector if it's big enough to get the axis
if (omegaMagnitude > EPSILON) {
axisX /= omegaMagnitude;
axisY /= omegaMagnitude;
axisZ /= omegaMagnitude;
}
// Integrate around this axis with the angular speed by the timestep
// in order to get a delta rotation from this sample over the timestep
// We will convert this axis-angle representation of the delta rotation
// into a quaternion before turning it into the rotation matrix.
float thetaOverTwo = omegaMagnitude * dT / 2.0f;
float sinThetaOverTwo = sin(thetaOverTwo);
float cosThetaOverTwo = cos(thetaOverTwo);
deltaRotationVector[0] = sinThetaOverTwo * axisX;
deltaRotationVector[1] = sinThetaOverTwo * axisY;
deltaRotationVector[2] = sinThetaOverTwo * axisZ;
deltaRotationVector[3] = cosThetaOverTwo;
}
timestamp = event.timestamp;
float[] deltaRotationMatrix = new float[9];
SensorManager.getRotationMatrixFromVector(deltaRotationMatrix, deltaRotationVector);
// User code should concatenate the delta rotation we computed with the current rotation
// in order to get the updated rotation.
// rotationCurrent = rotationCurrent * deltaRotationMatrix;
}
In practice, the gyroscope noise and offset will introduce some errors which need to be compensated for. This is usually done using the information from other sensors, but is beyond the scope of this document.
Sensor.TYPE_LIGHT:values[0]: Ambient light level in SI lux units
Sensor.TYPE_PRESSURE:values[0]: Atmospheric pressure in hPa (millibar)
Sensor.TYPE_PROXIMITY:
values[0]: Proximity sensor distance measured in centimeters
Note: Some proximity sensors only support a binary near or
far measurement. In this case, the sensor should report its
maximum range value in
the far state and a lesser value in the near state.
Sensor.TYPE_GRAVITY:A three dimensional vector indicating the direction and magnitude of gravity. Units are m/s^2. The coordinate system is the same as is used by the acceleration sensor.
Note: When the device is at rest, the output of the gravity sensor should be identical to that of the accelerometer.
Sensor.TYPE_LINEAR_ACCELERATION:The output of the accelerometer, gravity and linear-acceleration sensors must obey the following relation:
Sensor.TYPE_ROTATION_VECTOR:The rotation vector represents the orientation of the device as a combination of an angle and an axis, in which the device has rotated through an angle θ around an axis <x, y, z>.
The three elements of the rotation vector are <x*sin(θ/2), y*sin(θ/2), z*sin(θ/2)>, such that the magnitude of the rotation vector is equal to sin(θ/2), and the direction of the rotation vector is equal to the direction of the axis of rotation.
The three elements of the rotation vector are equal to the last three components of a unit quaternion <cos(θ/2), x*sin(θ/2), y*sin(θ/2), z*sin(θ/2)>.Elements of the rotation vector are unitless. The x,y, and z axis are defined in the same way as the acceleration sensor.
The reference coordinate system is defined as a direct orthonormal basis, where:
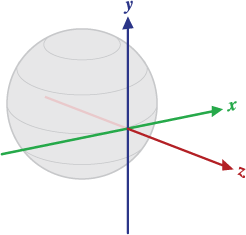
values[0]: x*sin(θ/2)
values[1]: y*sin(θ/2)
values[2]: z*sin(θ/2)
values[3]: cos(θ/2) (optional: only if value.length = 4)
Sensor.TYPE_ORIENTATION:values[0]: Azimuth, angle between the magnetic north direction and the y-axis, around the z-axis (0 to 359). 0=North, 90=East, 180=South, 270=West
values[1]: Pitch, rotation around x-axis (-180 to 180), with positive values when the z-axis moves toward the y-axis.
values[2]: Roll, rotation around y-axis (-90 to 90), with positive values when the x-axis moves toward the z-axis.
Note: This definition is different from yaw, pitch and roll used in aviation where the X axis is along the long side of the plane (tail to nose).
Note: This sensor type exists for legacy reasons, please use
getRotationMatrix() in conjunction with
remapCoordinateSystem() and
getOrientation() to
compute these values instead.
Important note: For historical reasons the roll angle is positive in the clockwise direction (mathematically speaking, it should be positive in the counter-clockwise direction).
Sensor.TYPE_RELATIVE_HUMIDITY:values[0]: Relative ambient air humidity in percent
When relative ambient air humidity and ambient temperature are measured, the dew point and absolute humidity can be calculated.
Dew PointThe dew point is the temperature to which a given parcel of air must be cooled, at constant barometric pressure, for water vapor to condense into water.
ln(RH/100%) + m·t/(Tn+t)
td(t,RH) = Tn · ------------------------------
m - [ln(RH/100%) + m·t/(Tn+t)]
for example:
h = Math.log(rh / 100.0) + (17.62 * t) / (243.12 + t); td = 243.12 * h / (17.62 - h);Absolute Humidity
The absolute humidity is the mass of water vapor in a particular volume of dry air. The unit is g/m3.
RH/100%·A·exp(m·t/(Tn+t))
dv(t,RH) = 216.7 · -------------------------
273.15 + t
for example:
dv = 216.7 * (rh / 100.0 * 6.112 * Math.exp(17.62 * t / (243.12 + t)) / (273.15 + t));
Sensor.TYPE_AMBIENT_TEMPERATURE:
values[0]: ambient (room) temperature in degree Celsius.